Die Fast Fourier Transformation (FFT) ist eine hochentwickelte mathematische Methode, die in vielen technischen Bereichen Anwendung findet, insbesondere im Bereich des Condition Monitoring und der Schwingungsanalyse von Maschinen und Anlagen. Dieser Artikel zielt darauf ab, ein tiefgreifendes Verständnis der FFT und ihrer Anwendungen im industriellen Kontext zu vermitteln.
Einführung in die Fourier Transformation
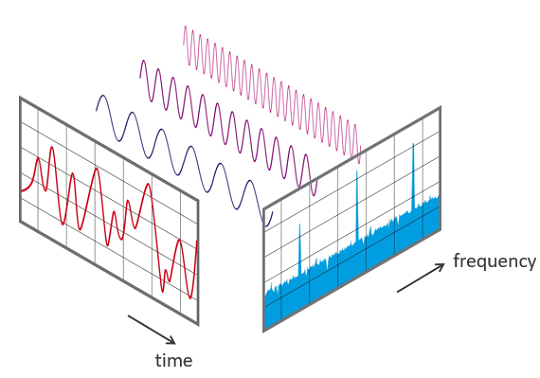
Die Grundlage der FFT bildet die Fourier Transformation, die von dem französischen Mathematiker Jean-Baptiste Joseph Fourier entwickelt wurde. Sie ermöglicht die Zerlegung eines zeitbasierten Signals in seine einzelnen Frequenzkomponenten. Diese Zerlegung ist essentiell, um periodische Vorgänge innerhalb eines Signals zu identifizieren und zu analysieren.
Von Fourier zu FFT
Die direkte Anwendung der Fourier Transformation in ihrer ursprünglichen Form ist rechenintensiv und zeitlich nicht effizient, besonders bei der Analyse von Signalen mit einer großen Menge an Datenpunkten. Die FFT ist eine algorithmische Optimierung, die eine deutlich schnellere Berechnung ermöglicht, indem sie die Symmetrien in den Fourier-Koeffizienten ausnutzt. Dies macht die FFT zu einem unverzichtbaren Werkzeug in der digitalen Signalverarbeitung.
Anwendung der FFT in der Schwingungsanalyse
Im Bereich der Schwingungsanalyse ist die FFT besonders wertvoll. Maschinenschwingungen entstehen durch eine Vielzahl von Ursachen, wie Unwucht, Fehlausrichtung, Getriebeschäden und viele andere. Jede dieser Ursachen erzeugt Schwingungen bei spezifischen Frequenzen. Durch die Anwendung der FFT auf Schwingungsdaten können diese charakteristischen Frequenzen identifiziert und somit die Ursache der Schwingungen diagnostiziert werden.
Prozess der Schwingungsanalyse mit FFT
1. Datenerfassung
Zu Beginn wird das zu analysierende Schwingungssignal mittels Sensoren erfasst. Diese Sensoren, oft Beschleunigungsmesser oder Schwingungsmessgeräte, wandeln die physikalischen Schwingungen der Maschine in elektrische Signale um. Die Qualität und Genauigkeit der Datenerfassung sind entscheidend, da sie die Basis der gesamten Analyse darstellen. Hierbei ist das Abtasttheorem von Nyquist-Shannon zu beachten, welches besagt, dass die Abtastrate mindestens das Doppelte der höchsten Frequenzkomponente des Signals betragen muss, um Aliasing-Effekte zu vermeiden.
2. Signalvorverarbeitung
Bevor die FFT angewendet wird, kann eine Vorverarbeitung des Signals notwendig sein. Dazu gehört unter anderem die Anwendung von Fensterfunktionen, wie dem Hanning- oder Hamming-Fenster, um das so genannte Leakage-Phänomen zu minimieren. Dieses Phänomen tritt auf, weil die FFT eine periodische Fortsetzung des Signals annimmt, was bei endlichen Signalen zu Verfälschungen führen kann. Fensterfunktionen glätten die Enden des Signals und reduzieren so die Auswirkungen von Leakage.
3. Anwendung der FFT
Nach der Vorverarbeitung wird die FFT auf das Signal angewendet. Mathematisch transformiert die FFT die Zeitreihe des Schwingungssignals in den Frequenzbereich, wodurch das Spektrum des Signals erhalten wird. Dieses Spektrum zeigt die Amplituden der verschiedenen Frequenzkomponenten des Signals und ermöglicht so eine detaillierte Analyse.
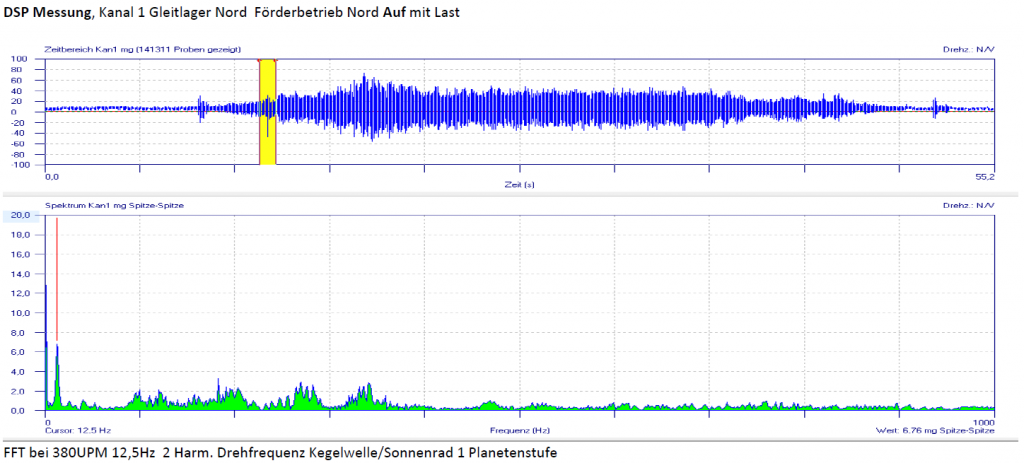
4. Analyse des Frequenzspektrums
Das Frequenzspektrum wird anschließend analysiert, um charakteristische Frequenzen und Muster zu identifizieren. Jede Komponente im Maschinensystem, wie Lager, Wellen oder Getriebe, hat typische Frequenzen, bei denen sie schwingen. Abweichungen von diesen normalen Frequenzmustern oder das Auftreten unerwarteter Frequenzen können auf potenzielle Probleme oder Defekte hinweisen.
5. Diagnose und Handlungsempfehlungen
Basierend auf der Analyse des Frequenzspektrums können Diagnosen gestellt und entsprechende Handlungsempfehlungen abgegeben werden. Beispielsweise kann eine erhöhte Amplitude bei der charakteristischen Frequenz eines Lagers auf einen Verschleiß oder Schaden hinweisen. Entsprechend können vorbeugende Wartungsmaßnahmen geplant und durchgeführt werden, um Ausfälle und kostspielige Reparaturen zu vermeiden.
Vorteile der FFT-Analyse
Die Fast Fourier Transformation (FFT) bietet in der Signalverarbeitung und Schwingungsanalyse eine Reihe signifikanter Vorteile, die sie zu einem unverzichtbaren Werkzeug in vielen technischen Disziplinen machen:
- Effizienz: Im Vergleich zur Diskreten Fourier-Transformation (DFT) ist die FFT aufgrund ihres Algorithmus wesentlich schneller. Die FFT reduziert die Rechenkomplexität, was besonders bei großen Datensätzen von Bedeutung ist.
- Frequenzaufschlüsselung: Die FFT ermöglicht eine detaillierte Zerlegung eines Signals in seine einzelnen Frequenzkomponenten. Dies erleichtert die Identifikation spezifischer Frequenzen und ihrer Amplituden, was für die Diagnose von Maschinenproblemen, wie Unwucht, Fehlausrichtung oder Lagerfehler, entscheidend sein kann.
- Zeitliche Effizienz: Aufgrund der Schnelligkeit der FFT können Schwingungsdaten in nahezu Echtzeit analysiert werden. Dies ermöglicht eine schnelle Diagnose und die Möglichkeit, proaktiv Wartungsmaßnahmen zu ergreifen, bevor größere Schäden oder Ausfälle auftreten.
- Verbesserung der Signalqualität: Durch die Anwendung von Fensterfunktionen im Vorfeld der FFT-Analyse können Leakage-Effekte und andere Artefakte, die die Signalqualität beeinträchtigen können, minimiert werden. Dies führt zu einer klareren und aussagekräftigeren Darstellung des Frequenzspektrums.
- Verbesserte Wartungsstrategien: Durch die präzise Analyse der Maschinenschwingungen können Wartungsstrategien von reaktiv zu prädiktiv oder sogar präskriptiv verschoben werden, was zu einer Optimierung der Betriebsabläufe und Kosteneinsparungen führt.
Herausforderungen der FFT Analyse
Bei der FFT-Analyse treten einige Herausforderungen auf, die das Ergebnis beeinflussen können. Eine allgemeine Betrachtung dieser Herausforderungen und der Ansätze zu ihrer Lösung umfasst folgende Punkte:
- Leakage-Effekt: Der Leakage-Effekt tritt auf, wenn das analysierte Signal nicht perfekt periodisch innerhalb des FFT-Fensters ist. Dies führt zu einer Verzerrung im Frequenzspektrum. Um dieses Problem zu mindern, können Fensterfunktionen wie das Hanning- oder Hamming-Fenster angewendet werden, die das Signal am Rand des Fensters sanft abfallen lassen und so die Auswirkungen des Leakage-Effekts reduzieren.
- Aliasing: Aliasing entsteht, wenn das Signal nicht mit einer ausreichend hohen Rate abgetastet wird, was zu einer Überlappung der Frequenzkomponenten führt. Die Lösung besteht darin, sicherzustellen, dass die Abtastrate des Signals das Nyquist-Kriterium erfüllt, d.h. sie muss mindestens doppelt so hoch sein wie die höchste Frequenz im Signal.
- Frequenzauflösung: Die Frequenzauflösung ist durch die Länge des FFT-Fensters begrenzt. Eine höhere Frequenzauflösung erfordert ein längeres Zeitfenster für die Analyse. Eine Alternative, um die Frequenzauflösung ohne Verlängerung des Aufnahmezeitraums zu erhöhen, ist das sogenannte Zero-Padding, bei dem das Signal künstlich mit Nullen erweitert wird, bevor die FFT durchgeführt wird.
- Dynamikbereich: Die FFT kann Schwierigkeiten haben, sowohl sehr große als auch sehr kleine Signalkomponenten gleichzeitig zu analysieren, was zu einem begrenzten Dynamikbereich führt. Dieses Problem kann durch die Anwendung von Skalierungstechniken oder durch die Verwendung spezieller Algorithmen, die für einen hohen Dynamikbereich optimiert sind, angegangen werden.
- Nicht-stationäre Signale: Signale, deren Eigenschaften sich über die Zeit ändern, können mit der herkömmlichen FFT schwer zu analysieren sein. Für solche Signale bietet sich die Verwendung der Kurzzeit-Fourier-Transformation (STFT) an, die eine zeitliche Lokalisierung der Frequenzkomponenten ermöglicht.
Die effektive Bewältigung dieser Herausforderungen erfordert ein tiefes Verständnis der Signalverarbeitung und der FFT-Algorithmik. Durch die Anwendung angepasster Fensterfunktionen, die Einhaltung des Nyquist-Kriteriums, die Verlängerung der Signale mittels Zero-Padding, den Einsatz von Skalierungstechniken und die Nutzung fortgeschrittener Analysemethoden für nicht-stationäre Signale kann die Qualität und Zuverlässigkeit der FFT-Analyse erheblich verbessert werden.
Schlussfolgerung
Abschließend ist die Fast Fourier Transformation (FFT) ein Schlüsselwerkzeug in der technischen Welt, besonders wertvoll für die Schwingungsanalyse und das Condition Monitoring. Ihre Anwendung ermöglicht präzise Einblicke in Maschinenzustände, wodurch Effizienz und Sicherheit in industriellen Prozessen signifikant verbessert werden.

